Genome Assembly for Hackers
This post collects code snippets I created while learning about genome assembly. I understand complicated things through code. I build simulations or little tools and they help me immensely to understand how something works. Probably because it uses vocabulary I am familiar with (python!) instead of domain specific jargon.
For another great example of "understanding X through code" check out Jake VanderPlas' talk Statistics for hackers (video).
This post covers the basic basics of "genome assembly". Starting with a genome, creating "reads" from it, breaking these reads up into "kmers", and then doing the actual assembly. There are a lot of subtleties that I gloss over, ignored details and ouright shortcuts (hashtag-physics-style). Please biology friends, don't hate me :)
I assume you have done some reading about this topic and came here to see it translated into code. I link to various wikipedia articles through out, but otherwise will not try and explain the biology reasoning behind all this (not just because I don't know it myself ...).
Let's start with generating a random "genome".
import copy
import string
import random
from itertools import product
from collections import defaultdict
import numpy as np
random.seed(123)
np.random.seed(321)
The Genome¶
We will use a fairly short genome made up totally at random. In reality genomes have millions or billions of base pairs and contain structure. Welcome to the world of "spherical cows in a vacuum".
genome = "".join(random.choice("AGCT") for _ in range(1000))
# this is a great genome, trust me
genome
Reading¶
To get the genome out of a cell you need to read it. This is called sequencing. While there are many methods to do this in an actual lab, in practice they all create "reads". These are short sections of the genome that cover a random part of it. To start with let's assume we can generate these reads without making any mistakes.
def perfect_reads(genome, n_reads=10):
"""Create perfect reads from `genome`"""
starts = np.random.randint(len(genome), size=n_reads)
length = np.random.randint(27,33, size=n_reads)
for n in range(n_reads):
low = starts[n]
yield genome[low:low + length[n]]
list(perfect_reads(genome, 3))
Reads can vary in size and come without information about where in the genome they took place. You can end up with duplicate reads of parts of reads overlapping. This is a good thing. These overlaps is what will allow us to piece everything back together. Read more about Shotgun sequencing
NB: Today most real world sequencing is done using "double barrel" shotguns. The key realisation is that you can create reads from both ends of a fragment of the genome. This way you gain some information about the direction of the reads relative to each other and how far they are apart.
Next each read is turned into a k-mer.
These are what is used during the actual assembly. k-mers are the substrings of
length k that you can generate from a string.
def kmers(read, k=10):
"""Generate `k`-mers from a `read`"""
for n in range(len(read) - k + 1):
yield read[n:n+k]
def get_perfect_kmers(genome):
kmers_ = []
for read in perfect_reads(genome, n_reads=1000):
for kmer in kmers(read):
kmers_.append(kmer)
return kmers_
kmers_ = get_perfect_kmers(genome)
# lots of kmers, but not that many are unique
print(len(kmers_), len(set(kmers_)))
With perfect reads from our random genome you end up with a
large number of k-mers (of length ten) but most of them
are duplicates. The roughly 20000 k-mers we created only
contain about 1000 unique k-mers.
Flipping reads¶
In reality the sequencing process is not perfect and will
make mistakes. The simplest way to illustrate this is to
randomly flip a base in a read. Even fairly low error rates
of 1% per base have a large effect on the number of unique k-mers
we find.
def flip(read, p=0.01):
"""Flip a base to one of the other bases with probability `p`"""
bases = []
for b in read:
if np.random.uniform() <= p:
bases.append(random.choice("AGCT".replace(b, "")))
else:
bases.append(b)
return "".join(bases)
def reads_with_errors(genome, n_reads=10):
"""Generate reads where bases might be flipped."""
starts = np.random.randint(len(genome), size=n_reads)
length = np.random.randint(27,33, size=n_reads)
for n in range(n_reads):
low = starts[n]
yield flip(genome[low:low + length[n]])
def get_kmers(genome):
kmers_ = []
for read in reads_with_errors(genome, n_reads=1000):
for kmer in kmers(read):
kmers_.append(kmer)
return kmers_
kmers_ = get_kmers(genome)
# roughly same number of kmers, but a lot more unique ones
print(len(kmers_), len(set(kmers_)))
We still generate roughly 20000 k-mers but now there are
three times as many unique k-mers. This is one of the factors
that makes assembling a genome so hard.
So now that we have a super simplistic model for generating
k-mers, how do we put them back together?
Assembly¶
Left as an exercise for the reader.
Just kidding. Assembly happens by creating
a de Bruijn graph
from our k-mers. Importantly each k-mer is represented
by an edge in the graph, not a node! Nodes are for k-1-mers.
If we have one 4-mer, abcd, the graph would look like this: abc -> bcd.
The first node represents the first n-1 symbols in the k-mer and
the second node represents the last n-1 symbols.
We will leave the world of biology behind for a moment and create completely artificial examples. I found this easier to understand and debug.
First we will need something that can turn a string into a graph.
Using k=2 the make_graph function will do just that.
def make_graph(string, k):
k_mers = list(kmers(string, k))
nodes = defaultdict(list)
for kmer in k_mers:
head = kmer[:-1]
tail = kmer[1:]
nodes[head].append(tail)
return nodes
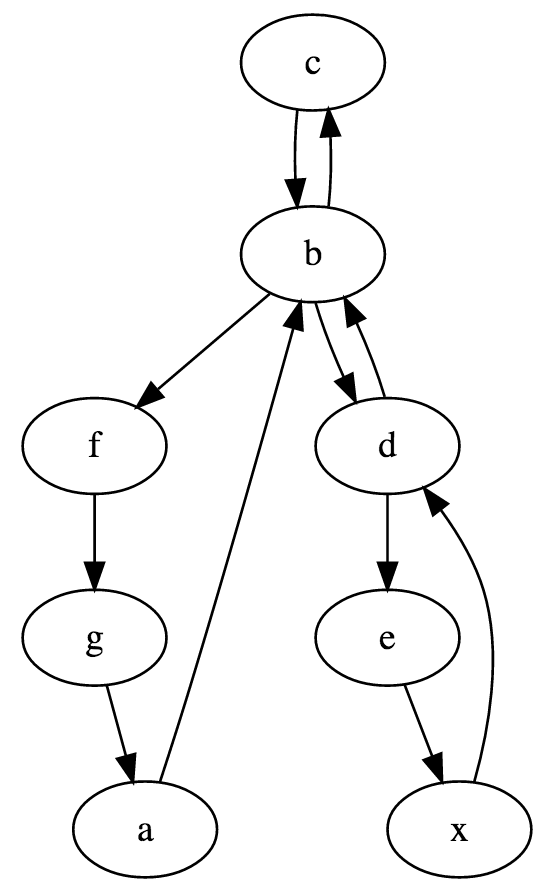
nodes = make_graph('abcbdexdbfga', 2)
print(nodes)
nodes is a dictionary mapping each node to the list
of outgoing edges for that node. Its printed representation
is quite ugly, so here is a graphical version of it:
You can render this with graphviz but this is not
installed on tmpbnb.org so will fail here.
from graphviz import Digraph
dot = Digraph(comment='debruijn')
for km1mer in nodes:
dot.node(km1mer, km1mer)
for src in nodes:
ends = nodes[src]
for end in ends:
dot.edge(src, end)
dot.format = 'png'
dot
Eulerian walks¶
Why create this weird graph structure from our reads? At first it seems like it makes things more complicated. Actually this is an example of transforming your problem to make it easier.
To reconstruct the original string from this graph all we have to do is find a trip along all the edges of the graph that visits each edge only once. If we can do that, we are done. People who are into graph theory call this an eulerian walk. If you grew up in Germany you might recognise this as solving the kids puzzle "Das ist das Haus vom Ni-ko-laus."

Von SoylentGreen - Eigenes Werk, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2308144
Is it a tour?¶
First things first, how will we know if a proposed tour is a valid one? This is what the next few functions take care of.
def edges(graph):
"""List all directed edges of `graph`"""
for node in graph:
for target in graph[node]:
yield (node, target)
def follow_tour(tour, graph):
"""Follow a tour and check it is eulerian"""
edges_ = list(edges(graph))
for start, end in zip(tour, tour[1:]):
try:
edges_.remove((start, end))
# most likely removing an edge that was already used
except:
return False
# if there are any edges left this is neither
# an eulerian tour nor an eulerian trail
if edges_:
return False
else:
return True
def check_tour(start, graph):
our_tour = tour(start, graph)
valid_tour = follow_tour(our_tour, graph)
return valid_tour, "".join(s[0] for s in our_tour)
To construct an actual eulerian cycle or trail we use Hierholzer's algorithm.
There are some subtleties we would have to take care of for a production grade implementation, like dealing with where to start when the graph only contains an eulerian path and not a cycle, etc. However it does the job for small examples and allows you to witness the miracle of genome assembly!
def tour(start_node, graph):
"""Find an eulerian cycle or trail.
This does not check if the graph is eulerian
so it might return tours that are nonsense.
"""
# _tour() modifies the graph structure so we need to copy it
graph = copy.deepcopy(graph)
return _tour(start_node, graph)
def _tour(start_node, graph, end=None):
tour = [start_node]
finish_on = end if end is not None else start_node
while True:
options = graph[tour[-1]]
# eulerian trail, not tour?
if not options:
break
tour.append(options.pop())
if tour[-1] == finish_on:
break
# when we insert a sub-tour we extend the
# length of tour, need to track this
offset = 0
for n,step in enumerate(tour[:]):
options = graph[step]
if options:
t = _tour(options.pop(), graph, step)
n += offset
tour = tour[:n+1] + t + tour[n+1:]
offset += len(t)
return tour
below some examples of graphs I tried out while writing the algorithm. This is an interactive blog post so play around with them. Use the snippet form above to draw each graph if you prefer to see it visually.
check_tour('a', {'a': ['b'], 'b': ['a']})
check_tour('a', {'a': ['b'], 'b': ['c'], 'c': ['a', 'e'], 'e': ['f'], 'f': ['c']})
check_tour('a', {'a': ['b'], 'b': ['c'], 'c': ['a', 'e'], 'e': ['f'],
'f': ['c', 'g'], 'g': ['f']})
check_tour('f', {'a': ['b'], 'b': ['c'], 'c': ['a', 'e'], 'e': ['f'],
'f': ['c', 'g'], 'g': ['f']})
check_tour('g', {'a': ['b'], 'b': ['c'], 'c': ['a', 'e'], 'e': ['f'],
'f': ['c', 'g'], 'g': ['f']})
check_tour('c', {'a': ['b'], 'b': ['c'], 'c': ['a', 'e'], 'e': ['f'],
'f': ['c', 'g'], 'g': ['f']})
random.seed(54)
genome = 'abcbdexdbfga'
g = make_graph(genome, 2)
valid, t = check_tour(genome[random.randint(0, len(genome)-1)], g)
print(g)
print(t)
I hope this helps you understand a bit more how all this genome assembly stuff works. it certainly helped me. If you know about the biology behind all this, please be lenient, if you spot gross mistakes or imprecise statements that cause confusion for novices do get in touch!
If you find a mistake or want to tell me something else get in touch on twitter @betatim
This post started life as a jupyter notebook, download it or view it online.